WyzGuys Tech Talk

Numbering Systems

By Bob Weiss

Many of the cybersecurity certifications that I teach have content that involves the uses of encoding, code injection, directory transversal, and scripting.  These concepts can be difficult to grasp, and the exam questions can be challenging to answer correctly.  This series of articles is designed to help you understand the basic concepts, and how these get used both securely and maliciously.  I am planning to show examples to help you identify these types of use cases or exploits when they show up in an exam question.

This is the first a multi-part series of articles.  We are going to start with the uses of binary and other numbering systems.  In the next article we will learn how these are used to create character sets of upper-case and lower-case letters, numbers, and symbols.  In the following articles, we will look at ways that encoding is used to modify or obfuscate web addresses and hyperlinks.  We will look at encoding as it is used in different command injection attacks, and directory traversal exploits.

One housekeeping tip:  If you click on the images, they will expand to full size on a separate tab.  You may then right click on the image and save it as a study aid.

Its All Numbers – Numbering systems

I always tell my classes that computers love numbers and hate letters.  Almost everything a computer is doing eventually is translated into bits or binary digits.  This is true for the letters of the alphabet, numbers, non-alphabetic symbols, as well as RGB color code values represented in pixels of an image.  Everything is converted into binary at some point.

Binary is the simplest of the four numbering systems used by computers.  It has two integers, 0 and 1.  It is useful in computer systems run by transistors which can be in one of two states, off or on (0 or 1).  Have you ever wondered about the logo etched in the power button?  It looks like a circle and a line, but it is a binary 0 and 1, off and on.

Here are the common computer numbering systems:

• Base 10 (decimal): 0-9 and place value powers of 10.  Not terribly useful for computers but most familiar system used by humans.  Binary is converted  by computers to decimal for humans to use.
• Base 2 (binary): 0 or 1 and place value powers of 2  Computers communicate in binary.
• Base 8 (octal): occasional use in computing (8 bits to a byte).  Handy for 7 and 8 bit systems such as ASCII and UNICODE which encode letters, numbers, and symbols.
• Base 16 (hexadecimal): Up to 16 values represented by 0-9 and A(10), B(11), C(12), D(13), E(14), and F(15).
  • 1 hex digit can represent 4 binary digits (a “nibble”)
  • 2 hex digits can represent 1 octet (1 byte or 8 bits)
  • 4 hex digits can represent 1 double-byte (16 bits) as in IPv6 addressing
  • Can be identified by leading 0x (0xFF) or trailing h for hexadecimal (FFh)
  • The numbers starting with 10 are represented by symbols that are similar to but are not the first six letters of the Roman alphabet.  These are NUMBERS and have numerical values.  The sooner you stop thinking of these as letters and start thinking of them as numbers, the easier hexadecimal will become for you.

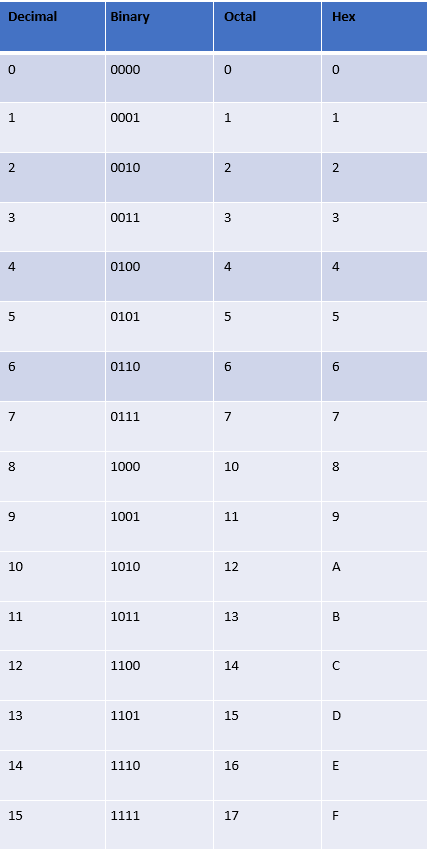
Here are the four numbering systems laid side by side

Binary, Octal, and Hexadecimal are all divisible by 2 and composed of powers of 2.  Since computers, processors, and transistors work in one of two states (on/off), these numbering systems are incredibly useful to computers.

Decimal is not.  In fact, Decimal numbering is almost useless to computers.  Decimal is used primarily by human computer users because we know decimal the best and use it the most.  Why?  As a species that has ten digits, five on each hand, and that uses those fingers for counting, it is obvious that humans developed decimal or Base 10 numbering as a biological convenience. Even the word digit can refer to a number or a finger.   If humans had eight fingers on each hand, we would have naturally developed and used hexadecimal for counting.

Let’s take a deeper look at Binary and Hexadecimal.

Binary Numbers

Binary is used all over the place in computing and networking.  It is used in IPv4 networking to calculate the identity of the host, the identity of the network, and to calculate the subnet mask, and determine the number of network segments and hosts each subnet mask can generate.

In the beginning of computing bits and bytes were precious and expensive, and so early character encoding schemes used only 7 bits, and sometimes only 6 bits.  These days we use 8 bit binary number or a full byte to represent a single character in character sets such as UTF-8.  We will look that that in the next article.

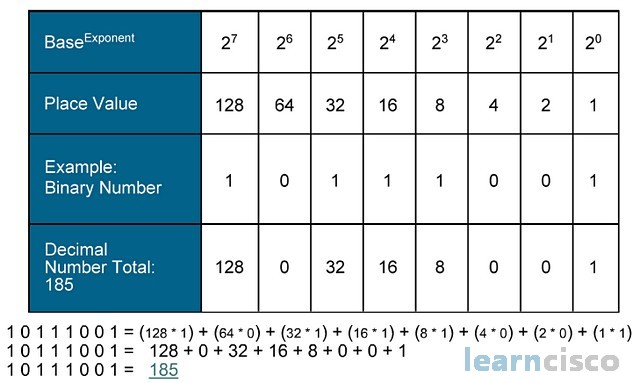
I think binary is relatively easy to learn, and I recommend that you do so.  The chart below shows 8 bit values that are used in both networking and character representation.  The binary zero is always equal to zero.  The value of the binary 1 depends on its position.  The least significant bit is the 1 in the far right column.  The most significant bit it the left hand most column.

Certification note: Manipulating the least significant bit in the binary RGB color codes is how a message can be hidden in an image.  This is called Steganography, and is covered in most cybersecurity exams.

In binary, the place value doubles each column to the left, or it halved in each column to the right.  In almost every way, binary is a simpler numbering system.

If all the positions in the chart contained a binary 1, the total value of the 8-bit binary number would be 128+64+32+16+8+4+2+1=255.

This chart is from LearnCisco.net

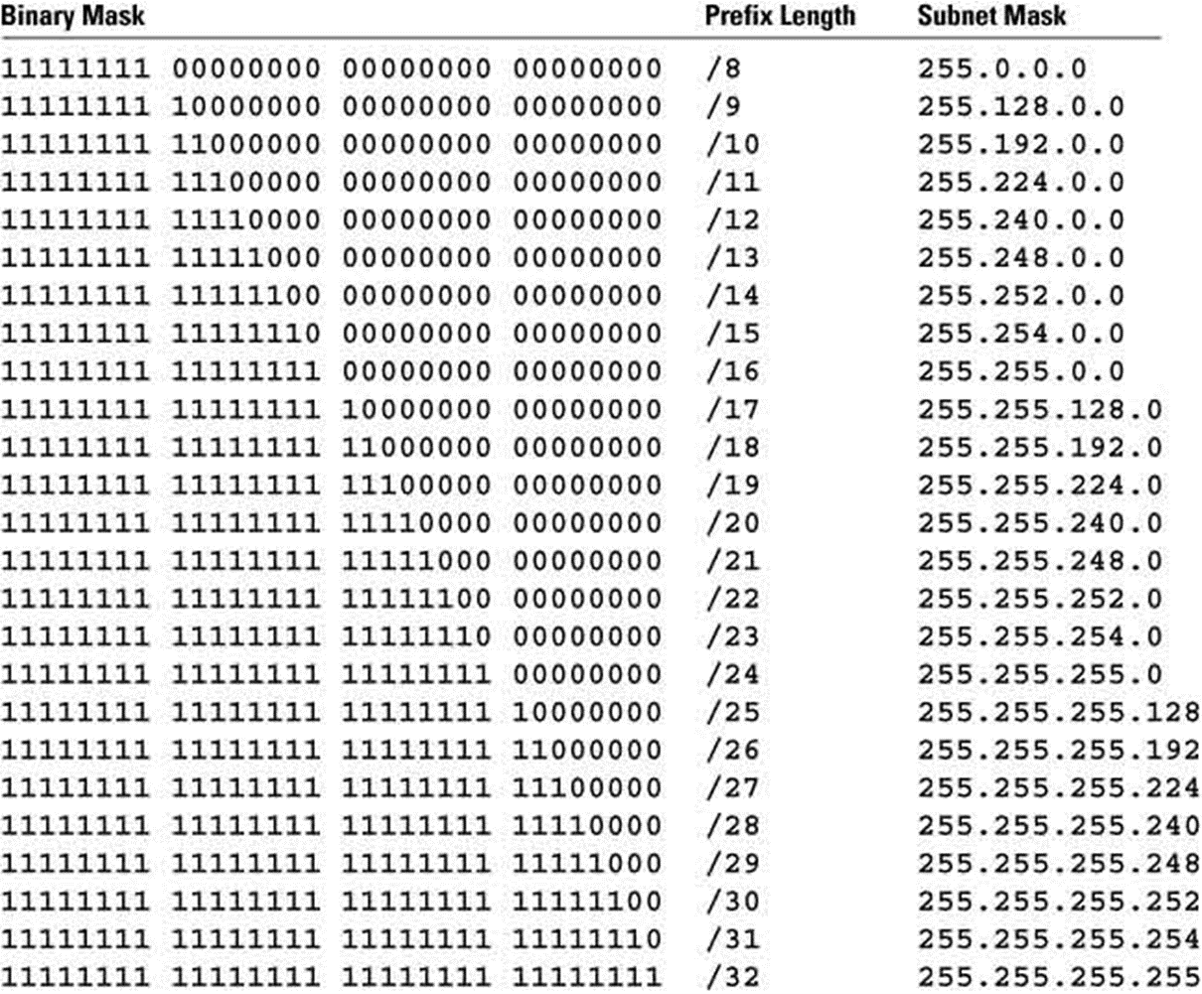
Here is a chart showing the complete range of subnet masks in binary notation, slash notation (CIDR or VLSM), and dotted decimal notation.  This is one place that you can learn to convert from binary to decimal and back.  The first 4 columns represent the binary values (Binary Mask) of the four octets of an IPv4 subnet mask.  The fifth column  (Prefix Length) is the “slash notation” of the subnet mask.  The number following the slash indicates the number of binary ones in the first four column, and is another way to show the subnet mask, and determine how many subnets and host you can get using a certain sized subnet mask.  The sixth column represents the dotted decimal equivalent of both the binary and slash notations

If I need 256, I would need a 9-bit number (100000000).  For most purposes 8-bits is enough, but if we need to express larger values over 255, we can use hexadecimal.  Hexadecimal is more compact and efficient.  In decimal the maximum value of an 8-bit binary number is 255.  In binary it is expressed as 11111111.  In hex it is FF (15 x 16) + 15

Hexadecimal Numbers

Let’s take a look at the hexadecimal numbering system.  Hexa plus decimal = 6+10 = Base16.  Even in naming we are unable to break free of our dependence on decimal.  Many of the charts and tables in this article series show equivalent decimal and hexadecimal numbers in adjacent columns, so we can know what the value of a hexadecimal number “really” is in decimal.  I encourage you to overcome your reluctance or difficulty with hex and learn how it works.  You will need it for a career in networking with IPv6, and it will come in handy other places where hex shows up in at work, such as  MAC addresses, error codes, encryption and encoding, for a short list.

Hexadecimal is comprised of sixteen numerical characters that run from 0 to F.  That is: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15). I want to reiterate:  the numbers starting with 10 are represented by symbols that look like but are not the first six letters of the English alphabet.  These are NUMBERS and have numerical values.  The sooner you stop thinking of these as letters and start thinking of them as numbers, the easier hexadecimal will become for you.

I created the chart below to help visualize how hex numbering works.  I of course have had to fall back on showing an adjacent row with decimal equivalents.

First the top 3 rows.  Row 1 shows the exponential expression of the powers of 16, row 2 is the hexadecimal expression of the number 1 in various places, and row 3 is the decimal equivalent.

• 16 to the zero power (column 5) is the “singletons” or the numbers ranging from 0 – F, just like in row 5.
• 16 to the first power (column 4) is equal to 16 x 1.  A 1 in this position has a value of 16.  A 2 in this position has a value of 2 x 16 = 32. as shown in row 8.
• 16 to the second power (column 3) or 16 squared is equal to 16 x 16 = 256 and is shown in row 11
• 16 to the third power (column 2) or 16 cubed is equal to 16 x 16 x 16 = 4096 and is shown in row 14
• 16 to the fourth power is shown in row 17.  This is equal to 16x16x16x16 = 65,536.  This interestingly enough is the total number of port numbers available to identify protocols of the TCP/IP stack.  Also the total number of addresses available in a class B network in IPv4 networking.

This table should give you a better grasp of the hexadecimal numbering system, and some of the ways it is used in computing and networking.  Here is a good site from Rapid Tables for converting decimal to binary to octal to hex and back.

In the next article we will learn how numbers are used to represent character sets of upper-case and lower-case letters, numbers, and symbols.  In the following articles, we will look at ways that encoding is used to modify or obfuscate web addresses and hyperlinks.  We will look at encoding as it is used in different command injection attacks, and directory traversal attacks.

Other Numbering Systems

These systems were not used in computing, but are interesting and important in there own way.

Duodecimal (Base 12)

An interesting but irrelevant point:  The ancient Egyptians used duodecimal or Base 12 for some reason.  Maybe the space aliens who helped them build the pyramids had six fingers, and taught the Egyptians to use Base 12.  LOL

Roman Numerals

[Update 2024-03-11]  I was recently reminded that humans used another numbering system that used alphabetical characters for numbers.  This would be Roman numerals, which was used extensively through the Roman Empire for hundreds of years.  Here is a chart of Roman numerals and their numeric values.

Hindu-Arabic Numerals

Roman numerals were replaced by the Hindu-Arabic number system, which is what we humans use for the decimal numbering system.  Roman numerals were great for counting things but not for mathematics, even simple things like adding and subtracting.  Originally from the Indian subcontinent, this system was brought west by Arab merchants.  Here is a chart of Hindu-Arabic numbers:

And then there was the invention of the ZERO!  We will save that for another time, but you might want to look it up on Wikipedia.

Sexagesimal (Base 60)

[Update 2024-03-19] Sumerians Looked to the Heavens as They Invented the System of Time… And We Still Use it Today. One might find it curious that we divide the hours into 60 minutes and the days into 24 hours – why not a multiple of 10 or 12? Put quite simply, the answer is because the inventors of time did not operate on a decimal (base-10) or duodecimal (base-12) system but a sexagesimal (base-60) system. For the ancient Sumerian innovators who first divided the movements of the heavens into countable intervals, 60 was the perfect number. The number 60 can be divided by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30 equal parts. Moreover, ancient astronomers believed there were 360 ​​days in a year, a number which 60 fits neatly into six times. The Sumerian Empire did not last. However, for more than 5,000 years the world has remained committed to their delineation of time.

Mayan Base 20

[Update 2023-08-25] – I read an interesting article on the Mayan Base 20 numbering system and copied it into Weekend Update]